I feel I understand
Existence, or at least a minute part
Of my existence, only through my art,
In terms of combinational delight;
And if my private universe scans right,
So does the verse of galaxies divine
Which I suspect is an iambic line.

"Pale Fire" by Vladimir Nabokov

Update your priors! It's a saying, drawn from Bayesian Statistics, which has fully arrived in the American vernacular, (at least for the podcast-listening crowd). Lately, I have even heard people describe some or another thing as "orthogonal to the discussion." Orthogonality, of course, is the unmistakable language of Linear Algebra. In real time, our language is being shaped by a new set of symbols, from statistics, probability, and matrices. A constellation of pursuits shaping up to be a new field! This new field has been called many things: Data Science, Machine Learning, Artificial Intelligence... We may settle on some other name in the future.

Of course, the future is already here—just unevenly distributed. The ruins of obsolete paradigms often crumble over years and lifetimes. Computer scientist and philosopher, Judea Pearl, in his books on Causality, totally blew apart the cliché-turned-dogma, "Correlation is not causation." We have all heard a thousand times what causation is not. Unfortunately, there is no catchy slogan for what it is... The truth is, correlation can be causation, given a properly constructed causal schema. Most people, even highly educated ones, are unaware of the currently-unfolding "Causal Revolution."

Cliché-busting is serious business. People have died over statistical definitions! Judea Pearl himself credits the late Barbara Burks with inventing the causal diagrams, which he has since made famous. Back 1926, Burks wrote the following remarkable critique, while researching the need for causal schematics:

"The true measure of contribution of a cause to an effect is mutilated if we have rendered constant variables which may in part or in whole be caused by either of the two factors whose true relationship is to be measured, or by still other unmeasured remote causes..."

In other words, there are different kinds of confounding, and it's bad news to control for confounding variables, which constitute the core mechanism of the relationship you're trying to understand. Burks was so far ahead of her time that she was unable to find work after completing her PhD. In the end, she jumped to her death from the George Washington Bridge in 1943, at the age of forty.

It takes a lot of courage to defy expert consensus. While I feel grief for Barbara Burks, I can see why her contemporaries may have been skeptical. The causal diagram seems almost too easy! Just erase some arrows and disambiguate others, and voila! It doesn't seem likely that the holy grail of statistics fits on a napkin? This would be almost too fortunate, like finding a bearer bond certificate worth millions in the attic.

Simplicity has its place, though, and if you want to see causality, it could be the case that you have nothing more to do, than look in the mirror.

In 1901, the German psychologist Karl Groos discovered through careful experimentation that infants are display extreme happiness when they first discover their ability to cause predictable effects in the world. Groos called this “the pleasure at being the cause,” and theorized that this joy is the motivation for play. Psychoanalyst Francis Broucek conducted a number of similar experiments, showing that children who delight in being a causal vector, if denied agency, become enraged, withdrawn, and even catatonic.

The counter-factual is a matter of removing arrows. When a child pours salt on a snail, or

I have two goals in this blog post, and they are ridiculously ambitious: (1) Clarify what causality is statistically and mathematically, and (2) clarify what causality is philosophically given what it is mathematically. The first goal requires us to conceive of the backbone of probabilistic reasoning. The second goal requires us to conceive of "reason" in the original sense of rationality. Rationality as a ratio of ratios, and causality as an added charge to a system, which ceases to be static, and moves instead.

From Aristotle's philosophical concept of Substance, to the ur-metaphor, to the concept of causality as laid out by Pearl, and the odds vector form of Bayes equation. They are all built upon, quite literally, the simplest logical structure imaginable. It's something I would have missed, had my Aristotle professor not drawn it on the board circa 2001. The logic is so simple that it's literally child's play. Children are iterating on the ur-metaphor all day everyday.

The Formal Cause

I was delighted to come across reference to Aristotle or Hume in my data science journey (see Causal Inference and Discovery in Python, by Aleksander Molak; see The Book of Why by Judea Pearl). It isn't often that philosophers find themselves relevant, and I happened to specialize in Ancient Greek and Early Modern European philosophy to boot. This is my wheelhouse, and I am over the moon that mathematicians and technologists have entered the discussion.

It all started in Aryeh Kosman's Aristotle class, circa 2001. Professor Kosman was a local legend. He taught the ancients, and even kind of looked like Socrates, except he wore khakis with socks and Birkenstocks. He could read Plato and Aristotle in the original Greek, and would often pause mid-sentence, to opine on the translator's choice of words. As an aside, he was good friends with Timothy Leary once upon a time, while a student at Harvard.

I remember on one particular occasion, a somewhat agonizing slog through Aristotle's Metaphysics, in which we all sat dumbfounded, as the professor went on about "actual potential" vs. "potential potential"...we were just not getting it. "You will understand Aristotelian Substance when you understand this," Kosman said as he walked up to board, chalk in hand, and drew the following:

"— : —"

Kosman returned to his chair and sat down. A long and awkward silence followed. What did it mean? Nobody was brave enough to venture so much as a guess.

There are many senses in which a thing is said to be. "Substance", according to Aristotle, is the primary mode of being. But why did Aristotle care about classifications of being? "You have to read the English translation (of the Greek) like they were speaking French," went another Kosman-ism. Translations of ancient texts are inherently awkward, I took this to mean. Without a historical deep dive, I can't say for sure what were the salient philosophical polemics of the time, but I know for certain that an adequate translation would not focus on classes of being. Instead, it would be something like, "What are the gravitational centers in the universe? Why does the world as we know it naturally organize itself into certain categories, objects, activities, and attributes ?"

This was metaphysics before physics, but it was also definitions before libraries. That things can be defined is simply taken for granted now. If you want to know what something is, for the most part, you can just "look it up," somewhere. Today "Being" is densely populated. Aristotle's inquiry had a purity to it, which it could never have today, I suspect. It's not just a question about being, it's a question about state. The cliché is always that Aristotelian essence is "form+matter" whatever that means. I always found that unhelpful. An object oriented programmer may sooner grasp the original meaning of primary substance than your average humanities student like myself.

Try this example: My daughter, who is six (almost seven) asked me the other day, "How am I not myself from yesterday?" You might also ask why your brain parses solid objects the way it does, when visual input has no borderlines. Or why objects lacking any geo-location or traceable origin in any specific brain (think unicorns or Justice), nonetheless persist. State is a memory of past events.

What does reality really consist of? Why is the world parsed and organized the way it is? These concerns may seem esoteric, but they are more relevant now than ever. In a world of subatomic particles, neurotransmitters, and thinking machines, it's all too easy to lose oneself. That was another of Kosman's pet concerns: Ego dissolution, loss of self. Fortunately, LLMs have made it easier than ever to articulate primary substance: Human beings are, and machines are not, in the sense of being the doer of the activity of being. In a way, this begs the question, but only because some questions demand to be begged.

According to Aristotle, Substance has the following traits:
1) Substances are those things that best merit the title "beings."
2) These beings are individual objects, in contrast with properties or events.
3) Substance is that of which other modes of being, or properties, are predicated. It is not predicable of anything else.
4) The species and genera reveal primary substance.

Another clue, which Professor Kosman liked to perplex us with, lay in a class of French verbs drawn from what French teachers often call the house of being. In French, certain verbs indicate transitions of state rather than actions—arrival, departure, birth, death—and these get special treatment in the past tense. Instead of using a form of "avoir" (to have), these verbs pair with "être" (to be) as their auxiliary. So, je suis arrivé translates literally to "I am arrived," rather than "I have arrived." English lacks this explicit hierarchy of being; our verbs don’t announce their metaphysical category.

Causality is like an modification of identity. The equation will look the same. Causality is something you bring to the equation from outside of it.

To this day, I still do not know the answer to Professor Kosman's riddle. But unlike then, I have a guess. As I have been studying the key mathematical concepts of data science, I have picked up on a few key insights:
1) Causality implies change
2) Change implies a before and after
3) Causality implies a counterfactual
4) A counterfactual implies change of change
5) Identity implies comparison

I encountered two equations, which immediately made me think of Dr. Kosman's drawing. When I see subtraction, I see a ratio. Ratios can be converted into differences in log space.

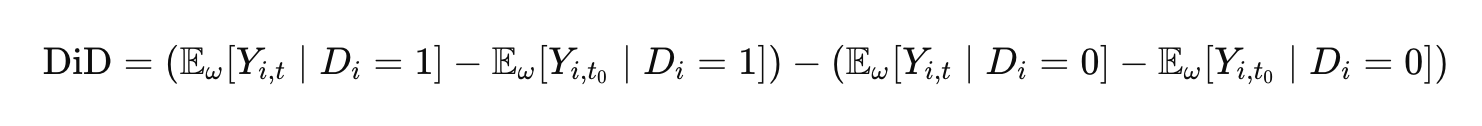
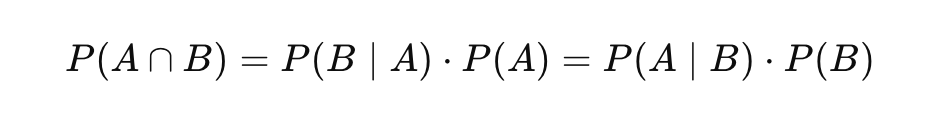
There are the identified and contrasted relationships, and there is the relating of those relationships. It's the colon, which represents the thing being identified. It is that which is parallel or similar. I immediately think of diff in diff, or the equation from which Bayes is derived.

. Classes model things that have properties and can cause things to happen. Each node in a causal diagram has state, and can cause things to happen in other nodes. In that sense, the DAG is like a network of class instances, passing messages to each other. Class is the genera. Object is the species. To have state means to have a form.

lilian_born = Human(nature)
lilian_grown = lilian_born.fit(nurture)

Judea Pearl shows us how we can use the same math that we use to demonstrate correlations—linear and logistic regressions, Bayesian networks, and non-linear models—to demonstrate causality. In an importance sense, the math does not change. It's the thrust of the math, which changes, and this "thrust" is documented in a causal diagram. If the diagram is correctly constructed, then truly causal claims can be made, using the traditional math of correlation. That is a big "if" and should not be trivialized. It's crucial to reason through the mechanism of causation prior to conducting statistical analysis.

I would say that Pearl's "do-logic" depends on the calculus of spirit, for lack of a better word. Causality, in other words, is a narrative. Correlation, difference in difference, and Bayes, are all species of causality, implicitly. While they may not be causal in particular instances, they merely fall short on a spectrum. A corollary to this argument is that causality is innate, displayed by child's play, and is a precondition to collecting data, before the "do" calculus ever comes into play. In other words, there is always an imagined counter-factual, and the counterfactual remains imagined, even when painstakingly reconstructed.

This is not where Pearl himself goes. He ends with a sort of weird and, to me, sudden pivot to "the illusion of free will," which is his species of "compatibalism." I may need to be forgiven for thinking that it's precisely because we can imagine counterfactuals that we are free. It's because we can intervene that we ascribe causality to the universe at all. Free will is a necessary condition for data, gathering, in my mind, and it's where I thought Pearl was going with his appeal to child's play. The child develops an intuition for causality concurrently to intervening.

The symbol that Kosman drew on the board, to me, represents the ur metaphor. In turn, the ur-metaphor is a genera with three species: (1) durable identity, (2) change, (3) causality. These are all the same, like the Father, the Son, and the Holy ghost. And they represent the reason we depart from the animal kingdom materially. We project the future. That doesn't mean the future has already happened. It depends, after all, on all of our interventions.

These, not coincidentally, map onto the three basic conditions for a causally-competent intelligence, which Judea Pearl outlines. (1) knowledge of the world (change), (2) knowledge of the self (durable identity), and knowledge of one's inner workings (causality, or consciousness). This empty identity, to me, expresses the now, which may be in state, or may be in process. The mathematical equations look the same, whether you consider P(A|do D) and P(A|D) because the do is you. You are causality. You can't see it because you are it. To me, this is merely what is meant by a "divine" will. There is nothing more banal than the poetry.

Humans by their nature project a matrix. It is in our being to "project causality onto" That matrix allows for temporality and counter-factuals. The matrix allows for durable identity, and by extension, for differentiation and organization. It allows for data collection. It allows for consciousness. The reason we could not see Causality is that it is an assumption behind the collection of evidence. By definition, the Bayesian equation can be nothing but a trip down a Möbius strip, but that does not make it any less informative. And look how far we have gotten by circling the Möbius strip! We have figured out how brains learn, insofar as they are machines. Causality was always a projection of ourselves, and ourselves were always a projection of causality.

Freshly emancipated from the pious avoidance of the fruit, of the Tree of Knowledge: Causality. The Mormons may be onto something when they say the Fall was not a sin, but a necessary step in coming to know God.

The Pearl origin myth is remarkable, especially because he opens his book with a tribute to Hume. He doesn't get it, and maybe that's to be expected, because he isn't a student of philosophy. No amount of repetition is going to imbue events with causal force. Similarly, no amount of repeated activity will turn a machine into a soul. The step change needed is a quantum leap. Additional vectors are required, which do not and cannot be explained with the logical resources of the equation itself. But at least he puts it out there as a confession:

"The ideal technology that causal inference strives to emulate resides within our own minds. Some tens of thousands of years ago, humans began to realize that certain things cause other things and that tinkering with the former can change the latter. No other species grasps this, certainly not to the extent that we do."

Closing myth: "In summary, I believe that the software package that can give a thinking machine the benefits of agency would consist of at least three parts: a causal model of the world; a causal model of its own software, however superficial; and a memory that records how intents in its mind correspond to events in the outside world." Just remarkable that he uses the phrase, "intents in its mind." Clearly he is just describing consciousness here.

Ending on a point of agreement: Judea Pearl reminds us that causal experimentation and counterfactual construction are literally child's play. We efface causality and fall back on correlation, because we erase ourselves in the process of establishing marginal probabilities, to begin with.

This blog post represents the story of how I got from the remedial version of Bayes Rule, to machine learning, to deep learning, to understanding AI. For those who struggle to memorize Bayesian formulas, as I always have, my hope is that this post pulls back the curtain on the math, so to speak, and leads to a fundamental understanding of the structure involved.

Getting from the odds vector form to the distribution form, gets you from simple associations to a ready understanding of causality. neural networks. Each Fourrier transform (DAG) converts dependence to variable outcomes, and intermediate layers that shut off nodes, introduce nodes, or transform coefficients, allows us to represent true causality.

A necessity, a will, a force a charge, a movement. Having state makes an entity capable of initiating interventions, i.e. causing change. Having state makes networks of entities capable of transmitting causality.